Spectral line profiles
In reality the spectral line under the influence of external conditions is broadened near its centre and can be represented in the form of a distribution curve shown in Fig.1.A distinction must be made berween the broadening of spectral lines under the influence of the Doppler effect (Doppler broadening) and the broadening due to collision of particles (Lorentz broadening). The first type of broadening is dominant at low pressures, for example, in the upper terrestial atmosphere, the second one at a higher but not very high pressure. The half-width of the spectral lines α(ij) is equal to the half of its width at half of maximum, as shown in Fig. 1.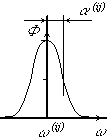
Fig. 1. Definition of half-width α(ij) in the line shape Φ(ω(ij) - ω).
The Doppler profile on Doppler broadening is represented by a Gaussian
ΦG(WNj, WN) = sqrt(ln2/π) exp(-ln2 · ((WNj - WN)/Dj)2)/Dj , (1)
where WNj is the position of jth line (ω(ij) on Fig. 1), WN - the current point on wavenumber axis, Dj -is a Doppler width for the jth spectral line
DJ = sqrt(2·ln2·NA·k·T/m) · WNj / c , (2)
where k is the Boltzmann constant, T is temperature (К), c - the speed of light, m is the molar mass of the isotopologue in grams and NA is the Avogadro constant.
The Lorentz profile can be represented as
ΦL(WNj, WN) = π-1 · Lj / ((WNj - WN)2 +( Lj)2) , (3)
where WNj is the position of jth line (ω(ij) on Fig. 1), WN - the current point on wavenumber axis, Lj -is a Lorentz width for the jth spectral line. The values of the Lorentz half-width at Tref and Pref of appropriate data source are represented in the database. In TheoReTS values of Lenv and Lself should be typed by a user in the Launch simulation form.
When there is simultaneous statistically independed effects of Doppler and Lorentz types of broadening, the profile of spectral line is a convolution of Doppler and Lorentz profile - a Voigt profile.
ΦV(WNj, WN) = ∫ ΦG(WNj, WN-x) · ΦL(WNj, x) dx . (4)
More sophisticated line shape functions are now being applied for for building of line profiles but they are not used in the system for a while.
